Introduction to Bernoulli’s equation and It’s Application

The Bernoulli’s equation is one of the most useful equations that is applied in a widevariety of fluid flow related problems.This equation can be derived in different ways, e.g. by integrating Euler’s equation along a streamline, by applying first and second laws of thermodynamics to steady, irrotational, inviscid and in-compressible flows etc.In simple form the Bernoulli’s equation relates the pressure, velocity and elevationbetween any two points in the flow field.It is ascalar equationand is given by:

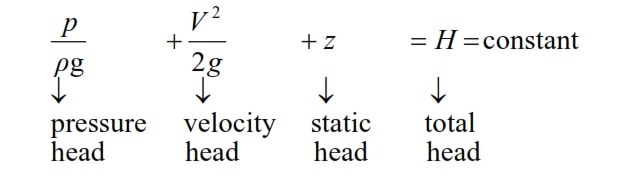
IntroductiontoBernoulliE28099sequationandIt27sApplication — 基本伯努利方程

Each term in the above equation hasdimensions of length(i.e., meters in SI units) hence these terms are called aspressure head, velocity head, static headandtotal headsrespectively.

Bernoulli’s equation can also be written in terms of pressures (i.e.,Pascals in SI units) as:

Bernoulli’s equation is valid betweenany two pointsin the flow field when the flow is steady, irrotational, in-viscid and incompressible. The equation is valid along a streamline for rotational, steady and incompressible flows. Between any two points 1 and 2 in the flow field for irrotational flows, the Bernoulli’s equation is written as:

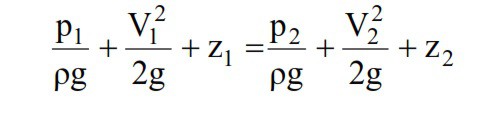
Bernoulli’s equation can also be considered to be analternate statement of conservation of energy (1stlaw of thermodynamics).

Refer this ;Fundamental laws of Thermodynamics

由于所有真实的流体都有有限的粘度，即在所有实际流体流中，因此在克服摩擦中会损失一些能量。这被称为头部损失，即，如果流体在垂直管中升高，则高度将比伯努利方程所预测的高。头部损失将导致流动方程式减小压力也意味着将一种形式的压力转化为另一种形式的可能性。For example,neglecting the pressure changes due to datum, it can be concluded from Bernoulli’s equation that the static pressure rises in the direction of flow in a diffuser while it drops in the direction of flow in case of nozzle due to conversion of velocity pressure into static pressure and vice versa. Figure 1 shows the variation of total, static and velocity pressure for steady, incompressible and inviscid, fluid flow through a pipe of uniform cross-section.方向。如果HEAD损失用H表示，则可以将Bernoulli方程式修改为：

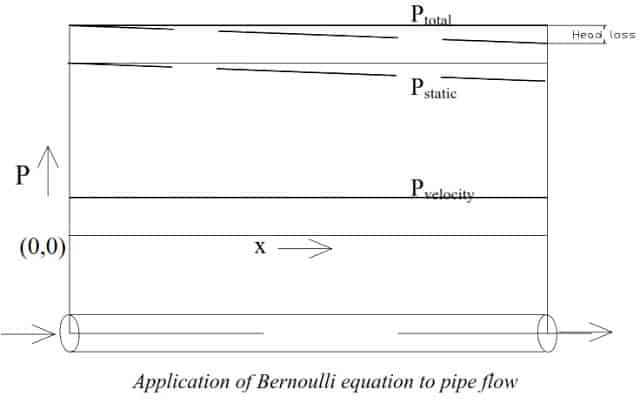
Fig 1. Application Of Bernoulli Equation.

Figure 1 shows the variation of total, static and velocity pressure for steady, incompressible fluid flow through a pipe of uniform cross-section without viscous effects (solid line) and with viscous effects (dashed lines)

More Resources /articles